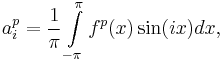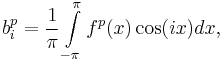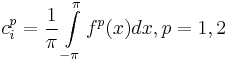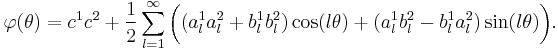Phase detector characteristic
A phase detector characteristic is a function of phase difference describing the output of the phase detector.
For the analysis of Phase detector it is usually considered the models of PD in signal space and phase space.[1] In this case for constructing of an adequate nonlinear mathematical model of PD in phase space it is necessary to find the characteristic of phase detector. The inputs of PD are high-frequency signals and the output contains a low-frequency error correction signal, corresponding to a phase difference of input signals. For the suppression of high-frequency component of the output of PD (if such component exists) the low-pass filters are applied. The characteristic of PD is the dependence of the signal at the output of PD (in the phase space) on the phase difference of signals at the input of PD. This characteristic of PD depends on the realization of PD and the types of signals at the input.
Contents |
Analog multiplier detector characteristic
Consider a classical phase detector implemented with analog miltiplier and low-pass filter.
Here 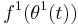 and
and 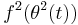 denote high-frequency signals, piecewise differentiable functions
denote high-frequency signals, piecewise differentiable functions 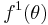 ,
, 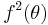 represent waveforms of input signals,
represent waveforms of input signals, 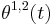 denote phases, and
denote phases, and 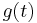 and denotes the output of the filter. If
and denotes the output of the filter. If 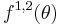 and
and 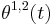 satisfy the high frequency conditions (see [2][3]) then phase detector characteristic
satisfy the high frequency conditions (see [2][3]) then phase detector characteristic 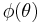 is calculated in such a way that time-domain model filter output
is calculated in such a way that time-domain model filter output
and filter output for phase-frequency domain model
are almost equal:
Sine waveforms case
Consider a simple case of harmonic waveforms 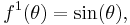
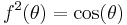 and integration filter.
and integration filter.
Standard engineering assumption is that the filter removes the upper sideband 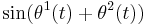 from the input but leaves the lower sideband
from the input but leaves the lower sideband 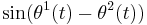 without change.
without change.
Consequently, the PD charaterstic in the case of sinusoidal waveforms is
Square waveforms case
Consider high-frequency square-wave signals 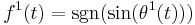 and
and 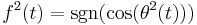 . For this signals it was found[4] that similar thing takes place. The characteristic for the case of square waveforms is
. For this signals it was found[4] that similar thing takes place. The characteristic for the case of square waveforms is
General waveforms case
Let us consider general case of piecewise-differentiable waveforms 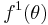 ,
, 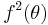 . In the case of simple integration filter, it's output is equal to
. In the case of simple integration filter, it's output is equal to
This class of functions can be expanded in Fourier series. Denote by
the Fourier coefficients of 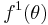 and
and 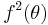 . Then the phase detector characteristic is
. Then the phase detector characteristic is
Obviously, the PD characteristic 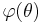 is periodic, continious, and bounded on
is periodic, continious, and bounded on  .
.
Modeling method based on this result is described in [5]
Examples
Waveforms 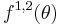 |
PD characteristic 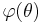 |
|---|---|
References
- ^ A. J. Viterbi, Principles of Coherent Communication, McGraw-Hill, New York, 1966
- ^ G. A. Leonov, N. V. Kuznetsov, M. V. Yuldashev, R. V. Yuldashev (2011). "Computation of Phase Detector Characteristics in Synchronization Systems". Doklady Mathematics 84 (1): 586–590. doi:10.1134/S1064562411040223. http://www.math.spbu.ru/user/nk/PDF/2011-DAN-Phase-detector-characteristic-Nonlinear-analysis-PLL.pdf.
- ^ N.V. Kuznetsov, G.A. Leonov, M.V. Yuldashev, R.V. Yuldashev (2011). "Analytical methods for computation of phase-detector characteristics and PLL design". ISSCS 2011 - International Symposium on Signals, Circuits and Systems, Proceedings: 7–10. doi:10.1109/ISSCS.2011.5978639.
- ^ G. A. Leonov (2008). "Computation of phase detector characteristics in phase locked loops for clock synchronization". Doklady Mathematics 78 (1): 643–645. doi:10.1134/S1064562408040443.
- ^ Patent RU 2011113212/08(019571)
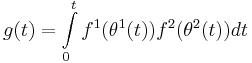
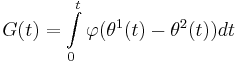
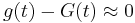
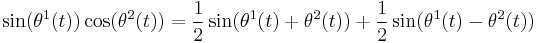
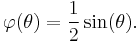
![\varphi(\theta) = \begin{cases}
1%2B\frac{2\theta}{\pi}, & \text{if }\theta \in [-\pi,0],\\
1-\frac{2\theta}{\pi}, & \text{if }\theta \in [0,\pi].\\
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/fa8124496de63893a88a5c85d586f568.png)